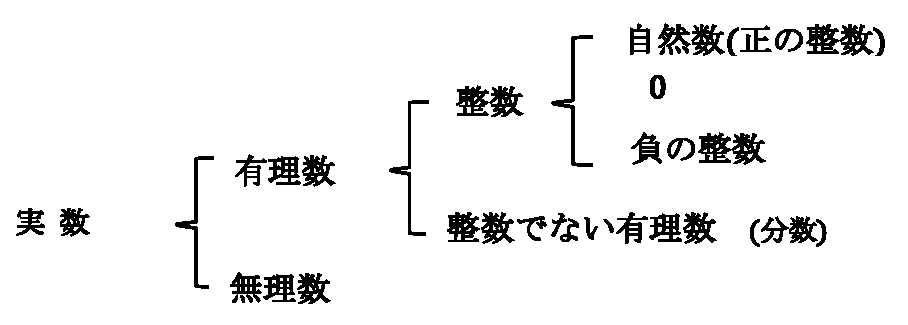
【補 足】
•上の体系図は見慣れた図ですね、特に疑問もなく当たり前のように見てますが、実数が明らかになるまでには長い歴史があったようです。この種の議論には深いもの(専門分野)があります。また数には複素数もありますが、これについてはどこかで扱うことにして、ここでは省きます。
•整数は、「割り算について閉じて」いないとは…
整数どうしの四足演算のなかで、以下の様に割り算での答えは整数にならないことがある。
\( 7+2=9 , \quad 9-2=7 , \quad 2 \times 8=16 \)…加・減・乗の答えは整数になる。
\(1 ÷3 =\frac{1}{3}\)…除算の答は整数にならない。
このことを「整数は割り算について閉じていない」と言う。
•有理数は、「四則演算において閉じている。」
有理数の演算は整数どうしの四足演算について、以下の様に答えは必ず有理数になる。
\(
2+ \frac{2}{3}=\frac{8}{3}\), \( 2-\frac{2}{3}=\frac{4}{3}
\)
\(4\times \frac{2}{4}=\frac{8}{4}\), \( \frac{6}{5}\)÷\( \frac{1}{2}=\frac{12}{5}\)
四足演算での答えは全て有理数である…このことを「有理数は四則演算についていて閉じている」と言う。
•数直線とは数直線上の点(大きさのない)と数が対応し(点の集まりの直線)…大きさががない点だから直線上を埋め尽せる。(直線上に数値が乗っているのではない)
•有理数と無理数には稠密性があるという性質……簡単にいうと、数直線のどんな狭い区間を取ってきてもその区間には有理数/無理数が存在するというような意味。
•また、実数には完備性(連続性ともいう)の性質があり、稠密性より密であり、ぎっしり詰まっているというようなイメージ。
完備とは…連続性についてのこと。
数の歴史は「自然数→整数→有理数→無理数→実数」のように拡張/拡大してきました。(さらなる新しい数がある可能性は?…数学者にお任せします)
実数の「完備性、連続性、コーシー列など」については解析学の分野です。
…ここではこの程度にしておきます。