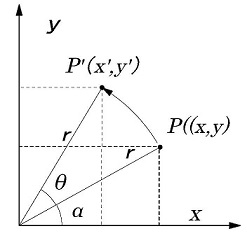
下図のxy直交座標において原点O を中心として点P(x,y)を角度θだけ回転させたとき点P'(x',y')とすると下式が成り立つ。
\((x,y)=(rcosα,rsinα)\)
\((x',y')=(rcos(α+θ),rsin(α+θ)\)
\(x'=rcos(α+θ)=r(cosα cosθ -sinα sinθ)\)
\(\quad =r cosα cosθ -rsinα sinθ \)
\(\underline{x'= xcosθ-ysinθ}\)
\(y'=rsin(α+θ)=r(sinα cosθ +cosα sinθ)\)
\(\quad =r sinα cosθ + rcosα sinθ= ycosθ+x sinθ\)
\( \underline{y'= xsinθ+ycosθ} \)
上式を以下の行列の積の形に変形します。
\( \begin{bmatrix} a & c \\ b & d \end{bmatrix}\)
\( \begin{bmatrix} x \\ y \end{bmatrix}\)
\( = \begin{bmatrix} ax + cy \\ bx + dy \end{bmatrix} \)
すなわち:
\( \begin{bmatrix} x’ \\ y’ \end{bmatrix}\)
\(=\begin{bmatrix} cosθ & -sinθ \\ sinθ& cosθ\end{bmatrix}\)
\( \begin{bmatrix} x \\ y \end{bmatrix}\)
この式の中の
\(R(θ)=\begin{bmatrix} cosθ & -sinθ \\ sinθ& cosθ\end{bmatrix}\)
として回転行列といいます。(反時計回り(CCW)が正)
時計回転り(cw)は負
\(R(-θ)=\begin{bmatrix} cos(-θ) & -sin(-θ) \\ sin(-θ)& cos(-θ)\end{bmatrix}\)
\( \quad =\begin{bmatrix} cosθ & sin(θ) \\ -sin(θ)& cos(θ)\end{bmatrix}\)
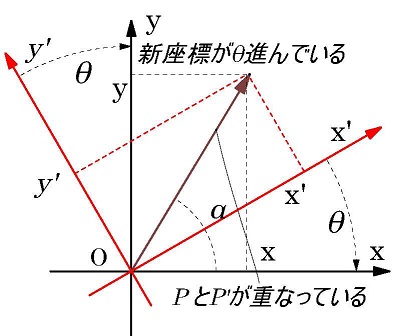
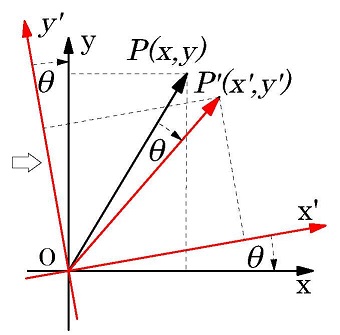
原点が同じで、元のxy座標より角度θをCCW方向に回転した新座標での点P'を考える。
座標変換には変換係数があります。
回転座標の場合は回転行列が座標変換になります。
元の座標の点Pが角度θをCCW方向に回転した新座標でP'です。
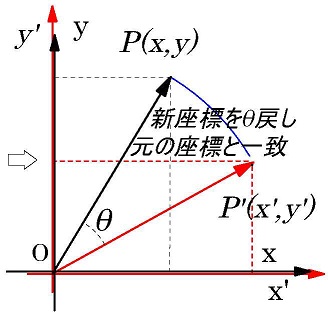
このことは新座標を角度θ、逆回転(CW方向)させ元の座標と同じすれば、
PとP’の角度はθとなります、注意すべきは、逆転させたので、回転行列は\(R(-θ)\)です。
すなわち:
\( \begin{bmatrix} x’ \\ y’ \end{bmatrix}\)
\( =\begin{bmatrix} cosθ & sinθ \\ -sinθ& cosθ\end{bmatrix}\)
\( \begin{bmatrix} x \\ y \end{bmatrix}\)
\(=R(-θ)\) \( \begin{bmatrix} x \\ y \end{bmatrix}\)