楽しく学ぶ数学…物理数学
曲面・接平面・全微分
(3次元空間)図1. 滑らかな曲面の全体
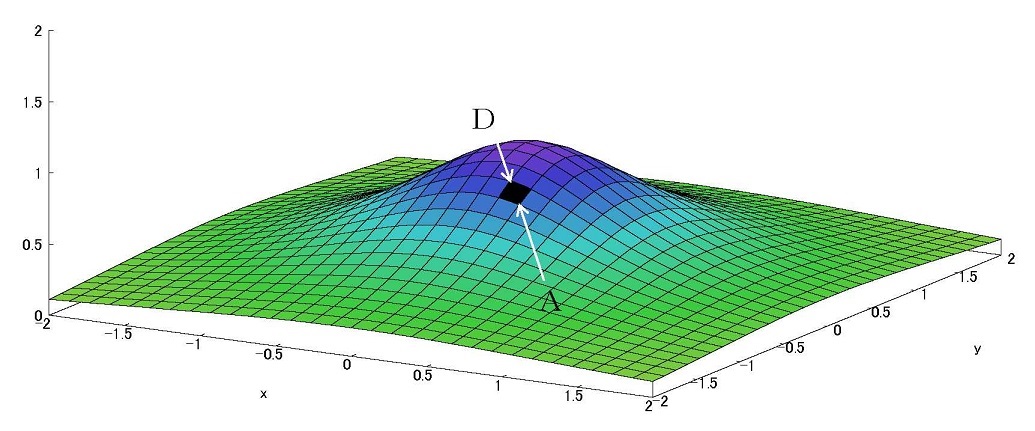
図2. 微小な接平面の拡大図
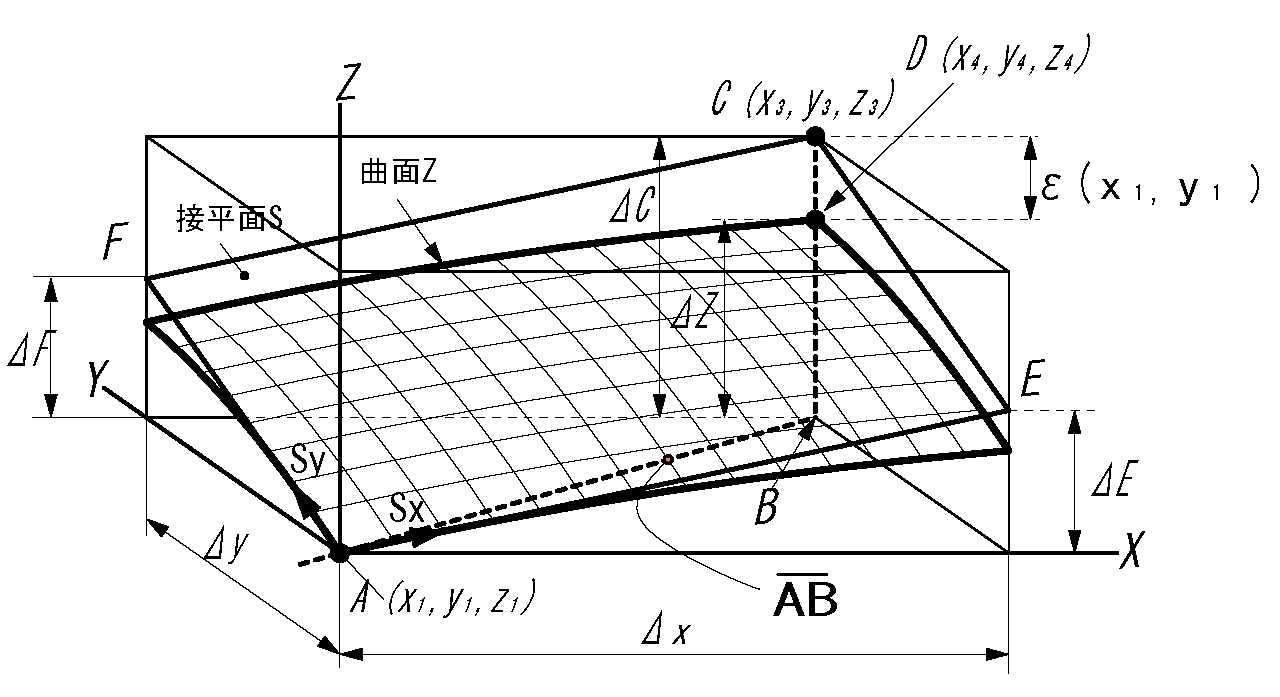
\( s_x ,\ s_y \) は単位接線ベクトル, その成分は\( s_x(1,0,m_x), s_y(0,1,m_y) \), また \( m_x, m_y \)は傾きです。
次式は\(f(x_1,y_1,z_1)\)を通る接平面の方程式です。
・この接平面は\( S_x\)と\(S_y\)のベクトルをもつ平面です。
・接平面となる条件は\(f(x,y,z)\)が\((x_1,y_1,z_1)\)で全微分可能であること。… 以下に説明します。
・以下の接平面に式は記号を替えて表わしています。
・また、ここではこの式の証明は省きます。
\(m_x=\frac{\partial f(x_1,y_1)}{\partial x} = f_x(x_1,y_1) \)
\(m_y=\frac{\partial f(x_1,y_1)}{\partial y}=f_y(x_1,y_1) \)
1変数(平面)の場合の「曲線と接線の方程式」の関係は2変数(空間)の場合は「曲面と接平面の方程式」が対応します。次式は\(f(x_1,y_1,z_1)\)を通る接平面の方程式です。
・この接平面は\( S_x\)と\(S_y\)のベクトルをもつ平面です。
・接平面となる条件は\(f(x,y,z)\)が\((x_1,y_1,z_1)\)で全微分可能であること。… 以下に説明します。
・以下の接平面に式は記号を替えて表わしています。
・また、ここではこの式の証明は省きます。
\[
f(x,y)-f(x_1,y_1) \]
\[
=\frac{\partial f(x_1,y_1)}{\partial x}(x-x_1)+\frac{\partial f(x_1,y_1)}{\partial y}(y-y_1)\]
\[
=f_x(x_1,y_1)(x-x_1) + f_y(x_1,y_1)(y-y_1)
\]
\[
= z-z_1= m_x(x-x_1) + m_y(y-y_1)=\varDelta z
\]
図3.上図(図2)のA-B-C断面
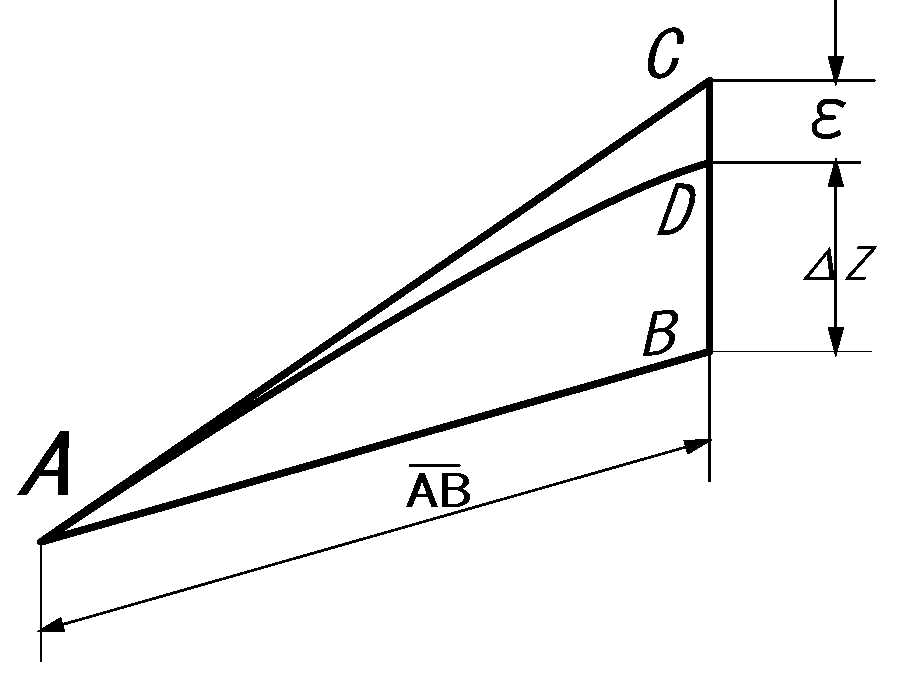
これから全微分について説明していきます。 その前に曲面の全微分可能性について見ていきます。
図2.より以下の式が作れます。
\[
\varDelta C=\varDelta E +\varDelta F =\]
\[\frac{\partial f(x_1,y_1)}{\partial x} \varDelta x +\frac{\partial f(x_1,y_1)}{\partial y} \varDelta y \]
\[ \ \ = f_x(x_1,y_1)\varDelta x +f_y(x_1,y_1)\varDelta y\]
\[
\varDelta z =\varDelta z - ε(\varDelta x,\varDelta y)\]
\(
=f_x(x_1,y_1)\varDelta x+f_y(x_1,y_1)\varDelta y-ε(\varDelta x,\varDelta y) \tag{1} \)
ε(\( \varDelta x,\varDelta y \))は曲面を接平面で近似してできるエラー(”ε” の読んで字の如し)、つまり誤差です。(\( \varDelta x,\varDelta y\))を限りなく0に近づけて、以下の式が0に収束すれば全微分可能であるという。
2次元の曲線と接線と同じ考え方です。
\[
\lim_{(\varDelta x ,\varDelta y) \to 0}\frac{ ε(\varDelta x,\varDelta y)}{\overline{A B}}
= \lim_{(\varDelta x ,\varDelta y) \to 0}\frac{ ε(\varDelta x,\varDelta y)}{\sqrt{ {\varDelta x}^2 +{\varDelta y}^2}}=0
\]
さてこれからこの全微分可能を前提にしていきます。 区間(\( \varDelta x,\varDelta y \) )を限りなく小さくし、\( \varDelta x →dx ,\varDelta y →dy ,\varDelta z =\varDelta f →df \)にして変形すると式(1)は下記の式になります。。
\[
df = f_x(x_1,y_1)dx +f_y(x_1,y_1)dy- ε({dx,dy})
\]
全微分可能であるから \( ε({dx,dy}) \)の項は0となり、全微分の式は以下となります。
\[
df = f_x(x_1,y_1)dx +f_y(x_1,y_1)dy \tag{2}
\]
\[
df= \frac{\partial f(x_1,y_1)}{\partial x} dx +\frac{\partial f(x_1,y_1)}{\partial y} dy \tag{3}
\]
変数が3つ以上の全微分式
以下の3変数の全微分式はf➝Uに変更、\((x_1,y_1,z_1 )\)は省略しています。
\[
dU= \frac{\partial U}{\partial x} dx +\frac{\partial U}{\partial y} dy+\frac{\partial U}{\partial z} dz \tag{4}
\]
なぜ”U”を使うかっていうと、コーヒーブレイクで紹介する力学のポテンシャル、熱力学のエネルギーを”U”を使うのが慣習だからです。
全微分の式を思いだす方法
図2の概念を理解し、次に、x軸で切った断面、y軸で切った断面のz方向の変化量の式の形を覚えいればよいのです。つまり、以下の形で□の中に変数x,yが入り、Δ➝dに替えれば全微分式です。
\[
\varDelta f = \frac{\partial \ f}{\partial \ \square } \ \varDelta \square \ + \cdots \cdots
\]
の形を思い出せれば全微分式が書けるはずです。

[コーヒーブレイク/閑話]…全微分の応用分野!
ここでは応用例の紹介のみです、何故?については専門の講義で説明します。
・ポテンシャルU(位置エネルギー),保存力f とすると仕事Wは次の通りです。
\[ f=(f_x,f_y,f_y)=( -\frac{\partial U}{\partial x},-\frac{\partial U}{\partial y},-\frac{\partial U}{\partial z}) \] \[ W=\int_{p_2}^{p_1} f\ \cdot dr\] \[ =\int_{p_2}^{p_1} (f_x dx + f_y dy + f_z dz) \] ここでUが全微分可能であるとすると \[ dU= \frac{\partial U}{\partial x} dx +\frac{\partial U}{\partial y} dy+\frac{\partial U}{\partial z} dz \] \[ \therefore W= - \int_{p_2}^{p_1} ( \frac{\partial U}{\partial x} dx +\frac{\partial U}{\partial y} dy+\frac{\partial U}{\partial z} dz ) \] このうように全微分が使われています。
また熱力学でも「エントロピー、温度、熱量、圧力、容積」などの状態変数が少し変化したときのエネルギーの増分についても全微分で表せます。これも熱力学の講義で説明したいですね!
学生の時に熱力のエントロピーが中々理解できずにいました。しかし、数十年後、また熱力学を学んで見ると、教材も良くなったか、理解が深まったと思います。
・ポテンシャルU(位置エネルギー),保存力f とすると仕事Wは次の通りです。
\[ f=(f_x,f_y,f_y)=( -\frac{\partial U}{\partial x},-\frac{\partial U}{\partial y},-\frac{\partial U}{\partial z}) \] \[ W=\int_{p_2}^{p_1} f\ \cdot dr\] \[ =\int_{p_2}^{p_1} (f_x dx + f_y dy + f_z dz) \] ここでUが全微分可能であるとすると \[ dU= \frac{\partial U}{\partial x} dx +\frac{\partial U}{\partial y} dy+\frac{\partial U}{\partial z} dz \] \[ \therefore W= - \int_{p_2}^{p_1} ( \frac{\partial U}{\partial x} dx +\frac{\partial U}{\partial y} dy+\frac{\partial U}{\partial z} dz ) \] このうように全微分が使われています。
また熱力学でも「エントロピー、温度、熱量、圧力、容積」などの状態変数が少し変化したときのエネルギーの増分についても全微分で表せます。これも熱力学の講義で説明したいですね!
学生の時に熱力のエントロピーが中々理解できずにいました。しかし、数十年後、また熱力学を学んで見ると、教材も良くなったか、理解が深まったと思います。