逆関数とその微分

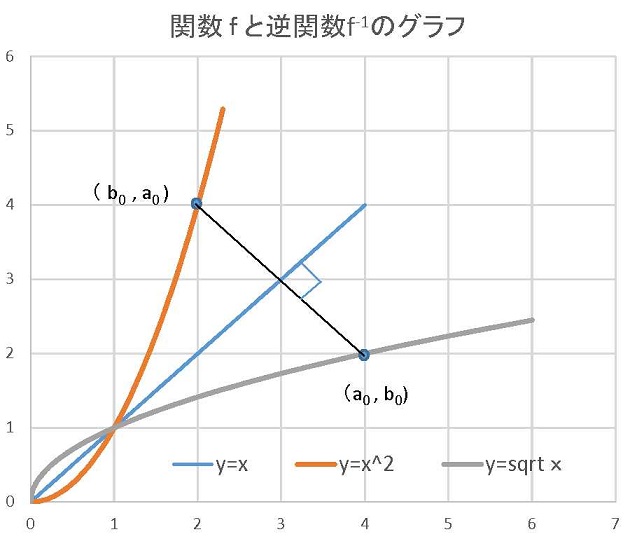
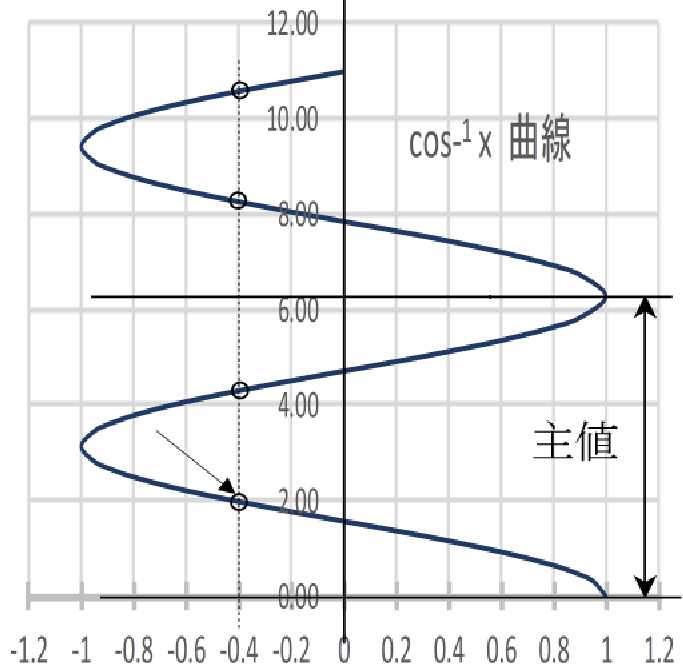
ここで逆関数の講義するのは、先に逆関数の微分積分が控えているからです。微分積分が苦手になるのも「逆関数の微積分」のところの人もいます。
ここで少しおさらいをします。…単調性について
数列に関して単調増加とは：
  数列{ \( {a_n} \) } に関し、\( a_1 \leq a_2 \geq　\cdots a_n \leq \cdots \)　のこと。
関数が\( f(x) \)が単調増加とは：
 \( x_1 \lt x_2 \) で \( f(x_1) \leq f(x2) \) が成り立つ場合。
関数が\( f(x) \)が狭義単調増加とは：
 \( x_1 \lt x_2 \) で \( f(x_1) \lt f(x2) \) が成り立つ場合。

・上では増加の説明でしたが、減少の方の…単調減少、狭義単調減少は\( x_1\lt x_2 \)に対して\( f(x) \)減少するものです。
・狭義があれば広義もありますね、狭義でない「単調増加/減少」が「広義」なのですが、通常この広義をつけてません。
・単に「単調」と言っている場合がありますが「文書の流れ」でこれらを判断するしかありません。
・関数 f(x) がある区間で連続かつ狭義単調であれば逆関数が存在します。

---

関数 y=f(x) は変数x に対しただ一つのy が決まり、逆にしてyを決めた時に x がただ一つ決まるときがあります。（決まる条件は書きの※1）
このとき x は y の関数となり　\( x=g(y) \) と表します。
関数\( x=g(y)\)の xとy を入れ替える操作します。➡\(　\ y=g(x) \)となります。
なぜ入れ替えるかは…独立変数をx、従属変数をy で表す慣習に従っているからです。
この\( y=g(x) \) を　\( f(x) \)の逆関数といいます。
一般\( f(x) \)の逆関数を\( f^{-1}(x) \)「fインバースx」と表します。
まとめると
\(　\ y=g(x)=f^{-1}(x) \)　となります。…　xとy を入れ替えている形です。
注：こような逆関数がある区間で存在する条件が上記のアンダーライン部(キーワードは…連続かつ狭義単調)です。
またその逆関数も連続かつ狭義単調となります。

例：\( y=\sqrt {x} \)の逆関数：
 \( x=y^2 \) 記号の入れ替えて次のようになる。
 \( y=x^2 \) …これが与式の逆関数。また \( y=g(x). \ y=f^{-1}(x) \) となる。 　　

逆関数のグラフ

下図は\(　\ y=x^2 \) とその逆関数\( y=\pm \sqrt{x} \)のグラフ(正の部分)です。
2つの関数は\( f(x)=x \)の直線に関して対称です。 関数\( f(x) \) のある点\( (a_0 , b_0) \)に対応する逆関数\( g(y) \)の点は\( (b_0 , ａ_0) \)です。
関数\( f(x) \)の\( (b_0)=f(a_0)　\)に対し逆関数のほうは\( (a_0)=g(b_0)　\)となります。
2点は互いにxとyが逆の関係にあり、それが\( f(x)=x \)という中線に関して対称となっています。

\( y=f(x) \)の逆関数を\( x=f^{-1}(y)=g(y)\)として\(\underline{ x=g(y)} \) と表せる。 両辺をxで微分すると（合成関数の微分を使う）：

となります。（上の2つの式は設問内容や微分のしやすさで決める）
さっそく次の例題に進み、実感してみましょう。

---

例 題

次の逆関数の導関数を求める。

　　

(1)\( y=\sin^{-1} x \ \)

　 \( y=\sin^{-1} x \) とすると\( \ x=\sin y \ \)と表せるので

　　

(2)\( y=\tan^{-1} x \ \)

\( y=\sin^{-1} x \) とすると\( \ x=\sin y \ \)と表せるので
定義域　(-∞< x < ∞)
以上より

---

[コーヒーブレイク/閑話］…主値とは(※1)