earth
湘南 理工学舎
[back]

 楽しく学ぶ…イプシロン・デルタ論法

 イプシロン・デルタ論法

 (ε・Ν論法)

関数の収束性や連続性を証明する方法がイプシロン・デルタ論法です。
関数が点\(a\)で連続とは、グラフでは点\(a\) でグラフがつながっていることです。
数学的には関数が点\(a\)で収束して極限値が存在することです。
その極限値があることを証明するのが\( ε・δ\) 論法です。
ここでグラフ示します。先にイメージ的に直感して下さい。
図の下に分かり易く説明しています。

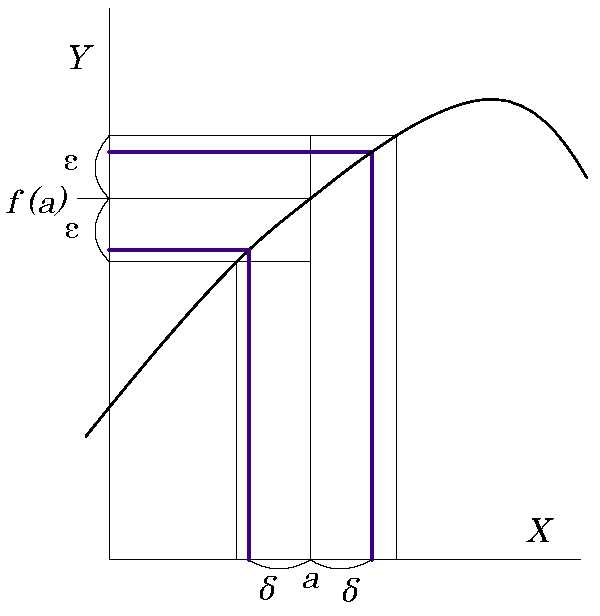
 【Fig.1 連続の場合1/2】εが大

ε・δ1

 【Fig.2 連続の場合2/2】 εが小　

ε・δ2

【Fig.1 解説】
はじめにどんな小さな\(ε\)をとっても、\(δ\)を十分小さくして（図では太線）、
\(|x-a|\)が\(δ\)より小さくなるようにすれば、
\(|f(x)-f(a)|\)は\(ε\)内に収まる。
すなわち、このことは：
\(0<|x-a|<δ \Rightarrow |f(x)-f(a)|<ε \)
となることがいえる。
注：はじめに\(ε\)を設定し、それに対応する（収まるような）\(δ\)を考える。

【Fig.2 解説】
さらに小さな\(ε\)をとっても、それにあった十分小さく\(δ\)をとれば\(|x-a|\)が\(δ\)より小さくなり、
\(|f(x)-f(a)|<ε\)となり、
\(0<|x-a|<δ \Rightarrow |f(x)-f(a)|<ε \)
となる。
このように、何回繰り返して、いくらでも「\(ε,δ\)」が小さくなり、\(|x-a|\)が\(δ\)より小さくなり
すなわち\(f(x)\)を\(f(a)\)にいくらでも近づけることです。 \(|f(x)-f(a)|<ε\)となり、
\(0<|x-a|<δ \Rightarrow |f(x)-f(a)|<ε \)となり
\(\underline{　\displaystyle \lim_{ x \to a} \ f(x)=α }\)

となる。…極限値が存在し、連続です

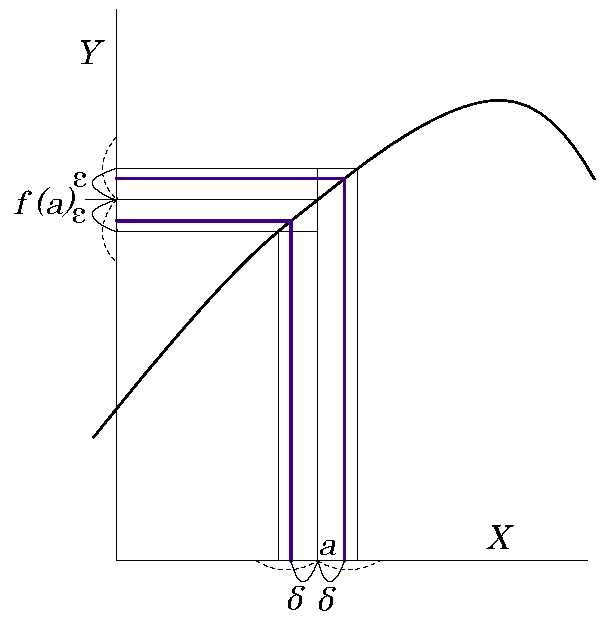
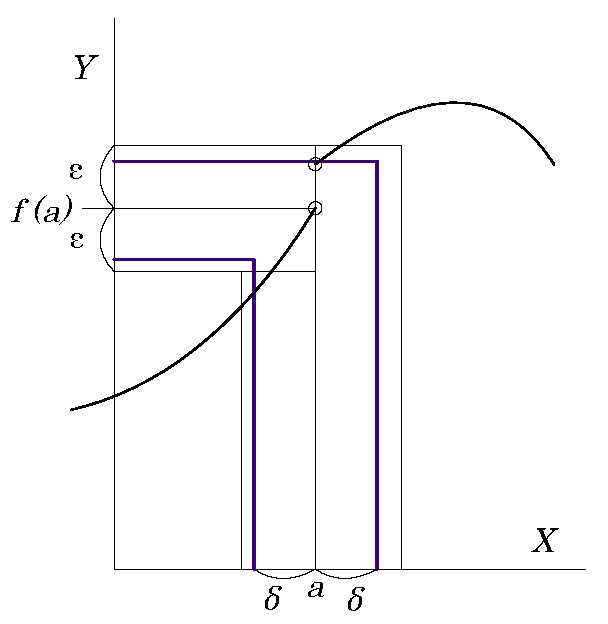
 Fig.3【不連続の場合1/2】　εが大

ε・δ1

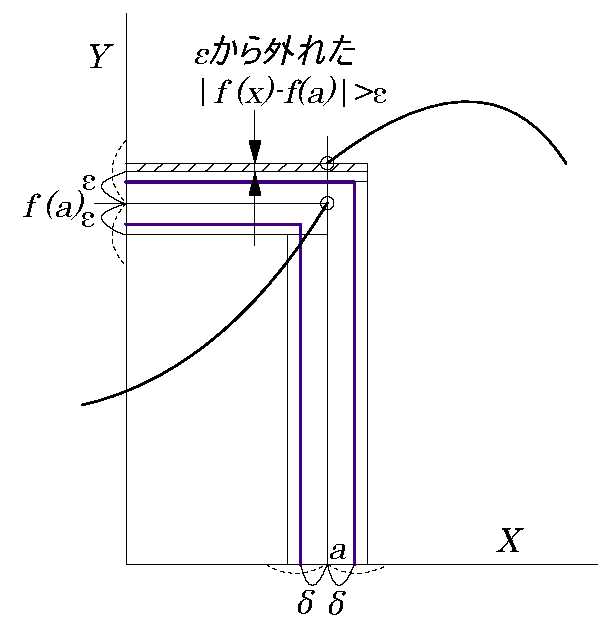
 【Fig.4不連続の場合2/2】　εが小

ε・δ2

　
【Fig.3 解説】
不連続な関数です。 \(ε\)が大きいときは連続と見える
しかし\(ε・δ\)論法では「\(ε\)は任意、ここではいくらでも小さな」
が条件です。　➝Fig4で不連続が判る。
【Fig.4 解説】
さらに小さな\(ε\)をとり、それにあった十分小さい\(δ\)をとると \(0<|x-a|\)が\(δ\)より小さくできるが
\( |f(x)-f(a)| \) が \(ε\) より外れてしまうこと、すなわち：
\(|f(x)-f(a)|<ε\)とることです。
極限値が存在せず、不連続であることが判る。
以上で\( ε・δ\) 論法の本質的なことは理解されたでしょう！
参考に高校での関数の極限の定義は：
xが限りなくaに近づき、f(a)が限りなく\(α\)に近ずくとき、\(α\)をf(x)の極限値という。
 \(\displaystyle \lim_{ x \to a} \ f(x)=α \) となる。　
ことでした。

\( ε・δ\) 論法を論理記号で表現すると：
\( ε・δ\) 論法
 \( \forall ε>0, \quad \exists δ \quad s.t.\)
\( \quad 0<|x-a|<δ \Rightarrow |f(x)-f(a)|<ε \)
 このとき　\(\displaystyle \lim_{ x \to a} \ f(x)=α \) となる。　
参考に論理記号の意味を書いておきます。
•\(\ \forall ε \)：「すべてのε （all）」または「任意のε　(any)」　
•\(\ \exists δ \)：「δが存在する　(exist)」　
•\(\ s.t.A \)：「Aのような　(such that)」
•\(\ A \Rightarrow B \)：「AならBである」　

【イプシロン・デルタ論法の分かり易いバージョン】　
\(\underline{ 0<|x-a|}\)より、変数\(x\)は\(a\)以外の値をとりながら\(a\)に近ずきます。
（上の下線は「\(x\)は\(a\)に近づくが、\(a\)にはならない」を意味している）
どんなに小さな正の数\(ε\)とっても、ある正の数\(δ\)が存在し、
\( a-δ<x<a+δ \)の範囲のx に対して、
\(|f(x)-f(a)|<ε\)　となるとき、
\(　\displaystyle \lim_{ x \to a} \ f(x)=α \) となる。
【例題】
(1)次式を\( ε・δ\) 論法により証明せよ。

 \(　\displaystyle \lim_{ x \to 5} \ 2x-5=5 \)

まず何を証明するか。
εは任意、δは与えれたεに従うが、まずは与式よりxを5に近付けることから\(\underline{ |x-5|}<δ\) として
\( ε・δ\)論法にあてはめる。すなわち：

 \( \forall ε>0, \ \exists δ \quad s.t.\)
\( \quad 0<\underline{|x-5|}<δ \Rightarrow |(2x-5)-5|<ε \)
を証明するのです。

\( |f(x)-f(a)|< ε \)
\(\ \rightarrow |(2x-5)-5| <ε\)

\( |(2x-5)-5|\)
\(\ =|2x-10|=2 \underline{|x-5|} <ε \)

（上の|x-5|<δ から上式はεとδの関係式に展開できる）

\( 2|x-5| <ε\)より\(2δ<ε\quad\therefore　δ <\frac{ε}{2} \)

このような\(δ\)において\( |2x-5-5|<ε　\)が成り立ち、証明ができました。

【確認】
求めた\(δ\)において
\( |f(x)-f(a)|\)が\(ε\)未満になることを確かめます。
 \(δ <\frac{ε}{2} \)より 今、 \(δ=\frac{ε}{3}\) とします。

\( |f(x\pm δ)-f(a)|\)
\(\ = |2(x\pm\frac{ε}{3})-5-5|\)
\(\ =|10\pm\frac{2ε}{3}-10|=\frac{2ε}{3}<ε\)

　
【例題】
(2)次式を\( ε・δ\) 論法により証明せよ。

 \(　\displaystyle \lim_{ x \to 2} \ x^2=4 \)

証明することは：
εは任意、δは\(\underline{ |x-2|}<δ\) として
（どんなに小さな\(ε\)に対しても…になるような\(δ\)が存在して…）
 \( \forall ε>0, \ \exists δ \quad s.t.\)
\( \quad 0<\underline{|x-2|}<δ \Rightarrow |x^2-4|<ε \)
です。　これから以下の式を抽出します。

\( |x-2|<δ \quad …(1) \)　
（\(x\)と\(δ\)の関係式です）

\(|x^2-4|<ε \quad …(2) \)

要は\(|x^2-4|<ε\) になるよう\(δ\)を求めればよいのです。(※1)

まず次が成り立ちます：
\(|x^2-4|= \underline{|x-2|}|x+2|<δ|x+2| \)

\(|x+2|\)を以下に展開します。

\(|x+2|=|x-2+4|=\underline{|(x-2)+(4)|}\)

\(\quad \underline{ \leq|x-2|+|4|}=δ+4\)

(上記は三角不等式を使っています）
したがって式(2)は：

\(|x^2-4|<δ|x+2|<δ(δ+4) \)

\(\qquad =δ^2+4 < ε\)

\( \therefore δ^2+4-ε <0 \)

これを解いて：

\(δ=-2 \pm \sqrt{4+ε} \)

\(δ\)は正の数なので\(\ δ=-2 + \sqrt{4+ε} \ \)です。
\(ε・δ\)論法を満足する\(δ\)を求めたことになります。（上記※1）
確認します。（詳細は省略）
\(\ δ=\frac{1}{2}(-2 + \sqrt{4+ε}) \ \)として：

\( |f(x)-f(a)|\)
\(\ =|\{x+\frac{1}{2}(-2 + \sqrt{4+ε})\}^2 - 2^2| \)

\( \ =ε-\sqrt{4+ε} <ε\)

イプシロン・デルタ論法にはあと２つのタイプがあります。
すなわち：
 \( \displaystyle \lim_{ x \to \infty} \ f(x)= A \)

 \(　\displaystyle \lim_{ x \to -\infty} \ f(x)= A \)

です。　これは数列のイプシロン・エヌ論法に似ています。
 \( \forall ε>0, \quad \exists δ>0 \quad s.t.\)
\( \quad x<δ \Rightarrow |f(x)-α|<ε \)
 このとき　\(\displaystyle \lim_{ x \to \infty} \ f(x)=α \) となる。　
 \( \forall ε>0, \quad \exists δ<0 \quad s.t.\)
\( \quad x<δ \Rightarrow |f(x)-α|<ε \)
 このとき　\(\displaystyle \lim_{ x \to -\infty} \ f(x)=α \) となる。　
【例題】
次式を\( ε・δ\) 論法により証明せよ。

\(\displaystyle \lim_{ x \to \infty} \ \frac{x}{x+1}=1 \)

（\( \quad f(x)=\frac{1}{1+\frac{1}{x}}\quad \) ）

\(|f(x)-1|<ε\)　

\(|\frac{x}{x+1}-1|<ε \)

\(\frac{1}{x+1}<ε \)

\( x>\frac{1}{ε}-1\) (途中省略)

\(\therefore δ>\frac{1}{ε}-1\ \)となる\(δ\)は存在し、

\( x>δ\) のとき\(|f(x)-1|<ε\)となる。

coffe

[コーヒーブレイク/閑話］…お疲れさまでした

【イプシロン・エヌ論法とイプシロン・デルタ論法】
イプシロン・エヌ論法は数列\( \{a_n\}\)（n:自然数） が離散的に変化して収束することを証明する方法。
イプシロン・デルタ論法は実数の変数\(x\)が連続に変化してある定数\(a\)に限りなく近づき、関数が収束することを証明する方法。

[back]