\(ε・N\) 論法を使わない高校では:
今、数列\( \{a_n\} \)、\( n \)は自然数(正の整数)に対し、次式があります。
\( \{a_n\}=\{\frac{1}{1},\ \frac{1}{2},\ \frac{1}{3},\ …\frac{1}{n},\ …\} \)
下式は数列の一般項です。
\( a_n= \frac{1}{n} \)
次の式は\( n \)を無限大にしたとき、\(0\) に収束する意味の式です。
\(\displaystyle \lim_{ n \to \infty } \frac{1}{n}=0 \cdots (1)\)
高校では数列\( n \)を
限りなく大きくしたとき、この数列は
限りなく0に近ずくとして:
\( \{a_n\} \)は0 に収束し、0 を数列\( a_n \)の極限値と言った。(極限値 \(α=0 \)です)
「限りなく近ずく」とは直感的、主観的です。
これなら馴れいて分り易いのですが、大学ではそうはいきません。
ε・N 論法が導入されます。
ε・N 論法での定義
\( n \):自然数、\(N\):自然数 \(ε\):実数
任意の正の数\(ε\)が与えられとき、ある自然数\(\ N\ \)が存在して、
\(n\)が\(n≥N\)ならば
\(|a_n-α|<ε \cdots (2) \)
が成り立つ\(\ n\ \)が、見つかるとき、
\(\displaystyle \lim_{ n \to \infty } \ a_n=α \)となる。
すなわち数列は収束して、その極限値は\(\ α\ \)であるといいます。
ε・N 論法の説明
以上が定義ですが、曖昧さがなく厳密・簡潔すぎて、難しいですね!
以下に詳しく説明します。
\(ε\) は小さな数です。(式(2)が意味しています)
\(\because \)\( \ ε \)(エラー)は\(a_n\)と\(\ α\ \)(目標値※)の差であり、小さいほど精度が高い。
(※:推測した極限値)
(最高の精度(ゼロ)なら\(a_n=\alpha \)となり\(\alpha\)数列の極限値になります。)
(これは数学的説明ではありません。)
任意とは 「
すべて、勝手な、どれも」などの意味です。
「任意の正の数\(\ ε\)」とは勝手な小さい数です。
今、次の数列を考えます:
\( \{a_n\}=\frac{1}{1},\ \frac{1}{2},\ \frac{1}{3},\ …\frac{1}{n},\ …\)
この数列の一般項は:
\( a_n=\frac{1}{n} \)
式(2)は次のようになります。
\( |a_n-α|<ε\) \(\rightarrow |\frac{1}{n}-0| <ε\quad \therefore n>\frac{1}{ε} \)
以下の説明ではnをNとしてNを求めます。
\( \frac{1}{n} \rightarrow \frac{1}{N}\)
として考えます。
(N が求まれば、\(n=N+1\)からn が求まる。)
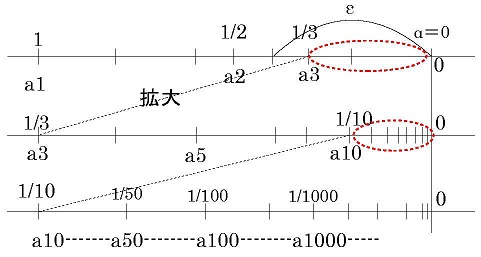
数列の番号 N を大きくすれば\( \{a_n\}\)はいくらでも小さくなります。
(下図は数直線上でイメージです、収束近辺を拡大して見るとεはいくらでも小さくでき、また1/an もいくらでも小さくできます)
例えば\(ε=0.1\)に対する\(N=\frac{1}{0.1}=10\)が存在しします。
また\(ε=0.01\)に対する\(N=\frac{1}{0.01}=100\)も存在します。
さらに\(ε=0.001\)に対する\(N=\frac{1}{0.001}=1000\)も存在します。
従って
どんなに小さな正の数εに対して
•いつもそれに対応できる数列の番号N が決められること。
•決めたN より後のすべての項\(a_{n+k}\)について、\(ε\)より小さくできる。
がいえます。
これよって
「限りなくαに近ずく」を使わないで
「数列がαに収束する」といえることになります。
証明にあってポイント:
•まず、n と \(ε\)の関係式を作る。
•この説明では具体的な数値を使いましたが、実際の証明には数値は使いません。
…説明終わり…